C/C++教學: 第二十四課 - 遞迴(Recursive)

Rain October 26, 2024

簡介top

這篇想介紹一下綜合了函式(Function)和鏈結串列(Linked List)的應用技巧 - 遞迴(Recursive)。

我們在介紹函式(Function)的文章中，在最後的注意事項裡有特別提到，所謂的遞迴(Recursive)就是函式呼叫函式本身，白話一點就是自己調用自己。

遞迴語法top

那麼，我們就先來看看構成遞迴的簡單範例:

void function (int a) {
    // do something
    function(a);
}
                        

如上範例，我們定義了一個函式叫做 function，在這之中可能做了一些計算處理，在這之後 function 又再調用了 function(自己本身)，像這樣我們就構成了遞迴(Recursive)。

遞迴應用top

回憶一下，我們在介紹鏈結串列(Linked List)的文章中，有介紹了結構(Struct)中的指標型成員(next)可以指向下一個節點。那麼，我們可以考慮一個應用情境，如下圖:

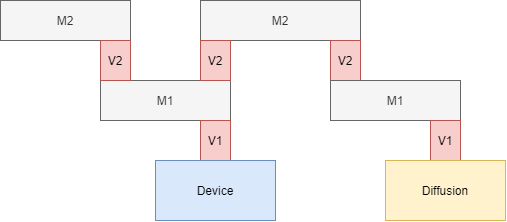
如上圖，假設我們需要判斷一個路徑，它能從 M 透過 V 一路走到 Device，並且將最長路徑返回，我們可以怎麼做呢? 看看下面的虛擬碼:

bool traversal(node* n, int& p)
{
    if (n == nullptr)
        return false;
    if (n->get_name() == "Device") {
        return true;
    }
    p++;
    for (const auto next : n->next_list) {
        int cp = p;
        if (!traversal(next, cp)) {
            p--;
            return false;
        }
        else {
            p = std::max(p, cp);
            return true;
        }
    }
    return false;
}
                        

我們可以設計一個走訪函式(traversal)，參數分別是節點指標(一開始為鏈結串列的起始節點指標)以及整數 p 作為計算總路徑長。

一開始我們就可以先判斷輸入進來的節點指標是不是空指標，若是的話則回傳 false 表示我們沒有找到目標，若已經找到我們的目標"Device"了，則回傳 true 表示我們已經找到目標。

若這些條件都沒有達成，表示這個節點不是 M 就是 V，代表路徑長度需要 +1，所以我們可以做 p++ 的計算。

接著，因為節點不是只有單一個 next (如圖示)，因此我們需要用一個迴圈把每個一個節點撈出來再丟給 traversal，這就形成了遞迴(Recursive)。當 traversal 回傳的值為 false 時，代表我們往下走的節點沒有找到目標，因此路徑長度需要退一步回上一個節點，若 traversal 回傳值為 true，則我們就可以和當前計算的路徑長度比較，得到最長的路徑。

其實這個例子不單純只是運用函式(Function)和鏈結串列(Linked List)，還有指標(Pointer)、傳址呼叫(Call by Address)和傳參呼叫(Call by Reference)，因此屬於比較進階一點的問題，初學者可能一時之間有點難消化。

但沒有關係，這篇的重點在於讓初學者理解，我們目前所介紹的內容到底可以如何應用並解決工程上的問題，可以先把這篇文章當作是應用介紹，稍微了解一下即可。

堆疊溢位(Stack Overflow)top

運用遞迴(Recursive)時，需要特別注意終止點為何，你可以發現到遞迴其實也有點類似迴圈，當函式不斷呼叫自己時，就也會導致無窮迴圈的發生。

那麼，什麼是堆疊溢位(Stack Overflow)呢? 程式在執行時，系統會給予程式一塊看似連續的記憶體空間，但其實它並不是連續的，因此我們稱它為虛擬記憶體(Virtual Memory)，這塊記憶體空間其中又有分為 Heap(堆積) 和 Stack(堆疊)。

當程式要執行函式的時候，記憶體位址會跳到 Stack 區段，是系統已經配置好的一個有上限的空間，而當遞迴(Recursive)執行沒有終點時，就會導致程式需要更多的記憶空間，而存取到超過 Stack 的上限位址，這就產生的堆疊溢位(Stack Overflow)。

類似的情況就像是我們介紹的靜態配置的陣列(Array)，當我們給予的索引(Index)超過原先配置給陣列的最大上限時，就代表存取到了一個不合規(Invalid)的位址。

下一篇: 第二十五課 - 列表(List)

Last updated: October 26, 2024